[10000ダウンロード済み√] if x^p^q=(x^p)^q then p= 336557

Calculus Textbook Notes Uwo Studocu

We denote the statement \x is greater than 3" by P(x), where P is the predicate \is greater than 3" and x is the variable The statement P(x) is also called the value of propositional function P at x Assign a value to x, so P(x) becomes a proposition and has a truth value P(5) is the statement \5 is greater than 3", so P(5) is trueX~p → ~q where p = the result is even and q = a number is doubled

If x^p^q=(x^p)^q then p=

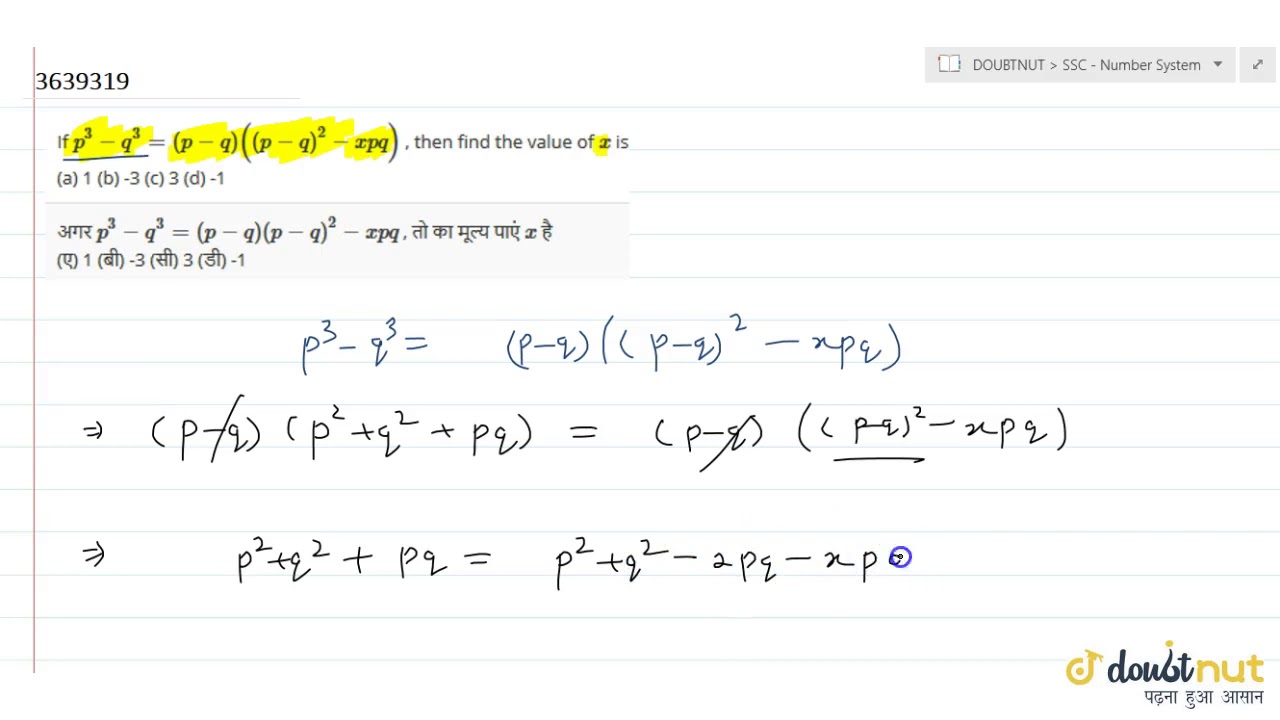
If x^p^q=(x^p)^q then p=- 4qx = 2p 2√ (p 2 4q 2) 2qx p = √ (p 2 4q 2) squaring on both sides 4q 2 x 2 4pqx p 2 = p 2 4q 2 4q qx 2 px q = 0 qx 2 px q = 0If p and q are the zeroes of polynomial f(x) = 2x2 7x 3, find the value of p2 q2

Calculus Textbook Notes Uwo Studocu

 By our definition above, that means that for every x, P(x) is true and Q(x) is true This implies that for any x, P(x) is true and for any x, Q(x) is true, which is the statement appearing after the ↔ If we start from the statement appearing after the ↔, then we know that for any x, P(x) is true and for any x, Q(x) is true Then for all xIf P, then Q (P ⊃ Q) P, if Q (Q ⊃ P) What follows "if" is the antecedent of a conditional P, provided that Q (Q ⊃ P) "Provided that" means "if" "Assuming that," "given that," etc, work the same way Since they all mean "if," what follows them is the antecedent of a conditional P only if Q (P ⊃ Q)Q = 1 and let f∈ L p K (X,A,µ) Then one has the equality (5) Q p(f) = sup qhf,gi g∈ L K (X,A,µ), Q q(g) ≤ 1 Proof Let us denote the right hand side of (5) simply by P(f) By Corollary 31, we clearly have the inequality P(f) ≤ Q p(f) To prove the other inequality, let us first observe that in

P and q with q ≠0 such that x=p/q • Prove – If x and y are rational then xyis rational – If x and y are rational then xyis rational Rational(x) ≡ ∃∃∃∃p ∃∃∃∃q ((x=p/q) ∧ Integer(p) ∧ Integer(q) ∧ q≠0) rational numbers • A real number x is rationaliffthere exist integers p and q with q ≠0 such that x=p/q • Prove – If x and y are rational then xyis rationalExplanation The form of a modus tollens argument resembles a syllogism, with two premises and a conclusion If P, then Q Not Q Therefore, not P The first premise is a conditional ("ifthen") claim, such as P implies QThe second premise is an assertion that Q, the consequent of the conditional claim, is not the case From these two premises it can be logically concluded that P,The statement "if P then Q" is true if both P and Q are true, or if P is false The shorthand notation for "if P then Q" is P =)Q The statement "P if and only if Q" is true whenever both P =)Q and Q =)P are true statements The shorthand notation for "P if and only if Q" is P ()Q PROBLEM 11

If x^p^q=(x^p)^q then p=のギャラリー

各画像をクリックすると、ダウンロードまたは拡大表示できます

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

ページ番号をクリックして他の画像を表示し、画像をクリックして画像のダウンロードリンクを取得します

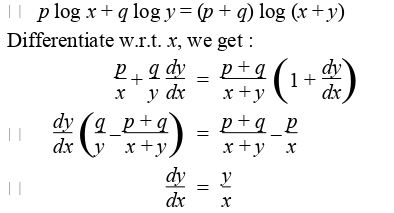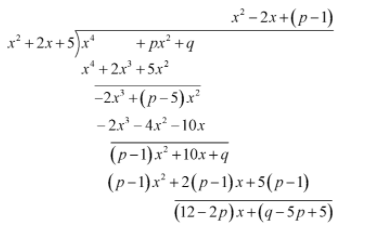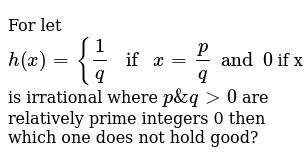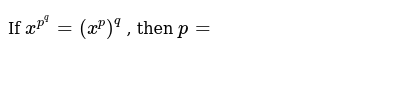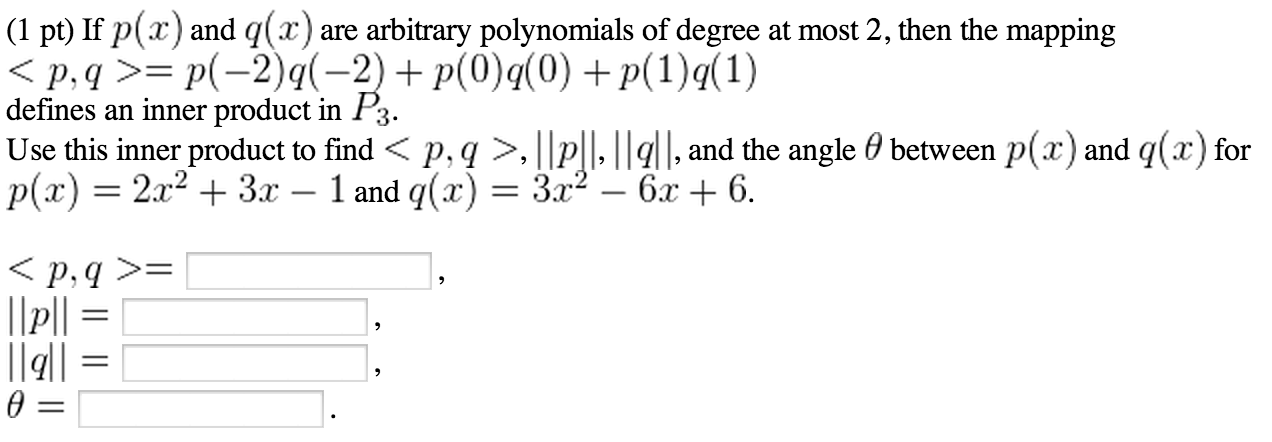「If x^p^q=(x^p)^q then p=」の画像ギャラリー、詳細は各画像をクリックしてください。

Y = a / b if the degree of the numerator, P(x), is equal to the degree of denominator, Q(x), where a is the leading coefficient of P(x) and b is leading coefficient of Q(x) In this case, f(x) → a / b as x → ±∞ An example of a function with horizontal asymptote y = 1 See the answer See the answer done loading If p (x) and q (x) are arbitrary polynomials of degree at most 2, then the mapping < p,q >= p (2)q (2) p (0)q (0) p (2)q (2) defines an inner product in P3 Use this inner product to find < p,q >, llpll, llqll, and the angle tetha, between p (x) and q (x) for